Sebagian dari kita, masih asing dengan
Graph. Program aplikasi satu ini umumnya digunakan para matematikawan dalam
membuat grafik berdasarkan persamaan yang dimasukkan ke dalamnya. Graph biasa
digunakan untuk membuktikan suatu persamaan apakah akan menampilkan grafik yang
diinginkan atau tidak.
Dari sinilah muncul ide untuk menggambar
sebuah objek menggunakan aplikasi Graph dengan cara memasukan berbagai persamaan
sehingga menghasilkan bentuk grafik yang unik, simple, dan nggak bikin mata
non-matematis sepet.
Ini bukan hal yang perdana loh, di berbagai
laman blog banyak para blogger yang sudah mulai mencoba melakukannya. Seperti Aria Turns dalam artikelnya tentang membuat persamaan
“grafik cinta”, atau seorang kawan bernama Haini
Pebriyanti dalam membuat grafik “Jembatan Ampera”.
Nah, kali ini, saya memilih bagian kepala
(termasuk wajah) Doraemon sebagai objek. Selain karena sangat suka tokoh kartun
legendaris ini, saya mempertimbangkan juga persamaan matematis yang relatif
mudah dari gambar ini. Nah, ayo kita mulai.
Pertama,
kita harus mencari model sebagai acuan kita dalam membuat persamaannya. Saya
pilih si Dora yang ini.
Kepala
2
buah lingkaran berdiameter 21 satuan dan 17 satuan
|
Hidung
1
buah lingkaran berdiameter 2 satuan
|
Mata
2
buah elips berukuran sama
|
Garis Hidung
1 garis lurus
|
Bola mata
2
buah lingkaran berukuran sama
|
Kumis
6 buah garis lurus
berukuran sama
|
Mulut
Setengah Elip
|
Setelah itu, baru kita bisa mulai menghitung letak/koordinat titik-titik setiap bagian penyusun gambar. tersebut. Langkah ini pastinya yang bikin kita pengen langsung SKIP aja :p
|
 |
Gambar 2: bikin di Corel Draw (no complain :p)
|
Persamaan
Lingkaran: (x-x1)2 + (y-y1)
= r2
Lingkaran Luar
Pusat (0,0)
diameter 21 satuan
Persamaannya:
= ( x – 0 )2
+ (y – 0)2 = 10,52
= x2
+ y2 = 110,25
|
Lingkaran Dalam
Pusat (0,-2) diameter
17 satuan
Persamaannya:
= ( x – 0 )2
+ (y + 2)2 = 8,52
= x2
+ (y + 2)2 = 72,25
|
Mata
terdiri dari 2 buah elips dengan ukuran yang sama (perhatikan gambar)
Mata
Mata kanan
|
Mata kiri
|
Bola Mata
Terdiri dari 2 buah lingkaran dengan ukuran yang sama
Persamaan lingkaran sudah disebutkan di atas.
Bola mata kanan
P= (2;6,5) radius = 1 satuan
Persamaannya:
(x - 2)2 + (y-6,5)2 = 12
(x - 2)2 + (y-6,5)2 = 1
|
Bola mata kiri
P= (-2;6,5) radius = 1 satuan
Persamaannya:
(x + 2)2 + (y-6,5)2 = 12
(x + 2)2 + (y-6,5)2 = 1
|
Hidung
Terdiri dari 1 buah lingkaran
Persamaan lingkaran sudah disebutkan di atas
Pusat (0;3,5)
diameter 2 satuan
Persamaannya
= ( x – 0 )2
+ (y - 3,5)2 = 12
= x2 + (y
- 3,5)2 = 1
Garis Hidung
Terdiri dari 1 buah garis lurus (Perhatikan Gambar)
Persamaan garis lurus :
Tapi untuk garis hidung ini, persamaan garis lurusnya
konstan yaitu:
x=0 dengan -6,5 < y < 2,5
Maksudnya berapapun ‘y’ nya, maka ‘x’ akan tetap nol.
Pada gambar ini, y
dibatasi lebih dari -6,5 dan kurang dari 2,5
Mulut
Terdiri dari
setengah elips
a=6,5 b=4
Pusat (0,-2,5)
Persamaan elips:

Kumis
Terdiri dari
tiga pasang garis yang berukuran sama
Persamaan
garis sudah disebutkan di atas
Kumis
Kanan
|
Kumis Kiri
|
Bagian atas: melalui titik (2,5;1,5) dan
(6,5;2,5)
dengan
2,5<x<6,5
|
dengan
-6,5<x<-2,5
|
|
--> 5y-2,5 = 0,5x-1,25
maka
persamaannya dapat ditulis: 20y-2x-7=0
dengan
2,5<x<7,5
|
Bagian tengah: melalui titik (-2,5;0,5) dan
(-7,5;1)
maka
persamaannya dapat ditulis: 20y+2x-7=0
dengan
-7,5<x<-2,5
|
Bagian bawah:
melalui titik (2,5;-0,5) dan (7,5;-1,5)
dengan
2,5<x<7,5
|
Bagian bawah:
melalui titik (-2,5;-0,5) dan (-7,5;-1,5)
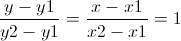
dengan
-7,5<x<-2,5
|
Nah,
setelah selesai mencari persamaan masing-masing bentuk, tinggal masukan
persamaan tersebut ke dalam program aplikasi Graph.
Cara
memasukannya, tekan f6 lalu akan muncul kotak dialog seperti gambar berikut:
Kolom Relation untuk
meng input persamaan yang dikehendaki, kolom Constraints untuk meng input syarat/batas interval (jika ada). Lalu
pilih OK. Input satu per satu
persamaannya hingga terbentuk grafiknya.
Kalau ada bagian grafik yang kurang sesuai, kesalahan pasti
terdapat pada persamaannya. Misal, tanda negative (-) atau (+), penggunaan koma
(,) atau titik (.), penggunaan tanda kurung {()} dan lain-lain. Atau mungkin
pada saat penginputan datanya. Yang jelas ini bukan salah Graph loooh.
Nah, THIS iS iT ! Doraemon in Graph! Selamat yaaa, kamu
berhasil :)
 |
| Doraemon in Graph |
 |
| ZOOMIN |
Thanks banget lah buat Equation Online -____-







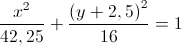










No comments:
Post a Comment
komentar capruk anda akan muncul setelah dimoderasi admin :)